What is Matrix Sketching?

Matrix sketching is a method of preserving some aspects of a large matrix in a much smaller one. For example, take some very large matrix \(A \in \mathbb{R}^{n\times m}\) where \(n\) or \(d\) or both are huge and represent it as a smaller matrix \(B \in \mathbb{R}^{\ell\times m}\) such that \(\|A - B\|\) is small. If you are familiar with the SVD an easy way to accomplish this would be to take the SVD and find the best rank-\(k\) approximation of \(A\) denoted \(A_k\). The problem here is sometimes we want guarantees on this approximation matrix but we don’t want the expensive \(\mathcal{O}(nm\text{ min}(n,m))\)computation of the SVD .

Frequent Directions to the Rescue!

Frequent Directions (FD) addresses both of these issues. FD is an algorithm invented by Edo Liberty.
It adapts the well known frequent items algorithm to matrices and provides some excellent guarantees on the relationship between the original matrix \(A\) and the sketched matrix \(B\). More formally, the algorithm takes in a stream of \(A\)’s rows and maintains a sketch of a matrix \(B\) with \(\ell << m\) where:\begin{align} B^TB \prec A^TA \text{ and } ||A^TA-B^TB||_2 \leq 2||A||_f^2/\ell \end{align} The matrix \(B\) can also be obtained in \(\mathcal{O}(\ell m)\) time and space. Which is considerably better than SVD. For a derivation of this bound and its complexity see the original paper PDF.

Experiments

I wanted to see for myself that the above bound holds in practice. To do this I performed FD on a matrix \(M\in \mathbb{R}^{10000\times 100}\) for \(\ell = \{50, 55, ..., 100\}\) and graphed the upper bound and \(||A^TA-B^TB||_2\) in Figure 1. Indeed we see that \(||A^TA-B^TB||_2 \leq 2||A||_f^2/\ell\)

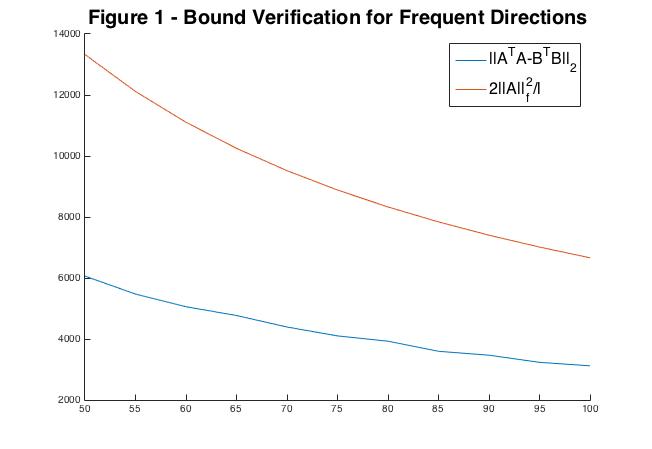
Next I wanted to see that FD is faster than SVD so I fixed \(\ell = 75\), \(n = 100\), and varied \(m\) from \(10000\) to \(100000\). The results are displayed in Figure 2.

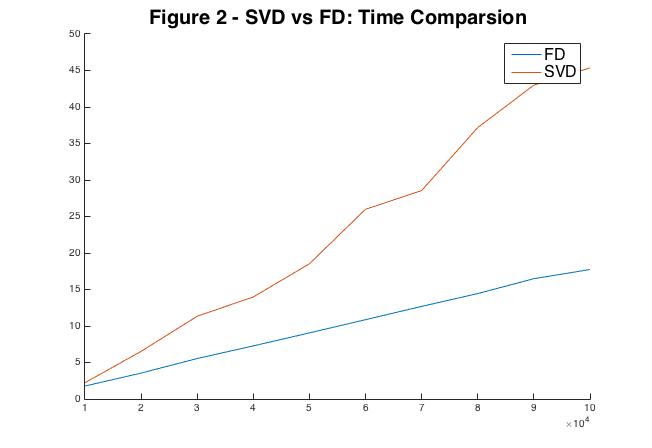
You can find my Scala implementation of Frequent directions along with my experimental code at: FD Implementation.