Convergence Tolerance
What is Convergence Tolerance?
I was recently asked why a large convergence tolerance is often practical in many machine learning settings so I decided to make a post on it. First off let’s understand what convergence tolerance is. Assume there is some function \(f(x)\) and we want to find the minimum. Let’s say that we have a starting point \(x_0\) and a way of calculating the gradient \(\nabla f(x)\). We can find the minimum by taking small steps in the direction opposite of steepest assent i.e.: \(x_{t+1} = x_t - \eta \nabla f(x)\) where \(\eta\) is a small number defining how big of a step we take at each iteration. For sufficiently small \(\eta\) this algorithm is guaranteed to converge, but in practice we don’t want to take \(\eta\) to be that small and even if we did the probability that \(x_t\) moves to the EXACT minimum of the function is in essence 0. This means we need some other way of defining convergence. The most natural, and the one that we will use here, is saying that we have converged when \(|f(x_{t})-f(x_{t-1})| < \epsilon\) for some \(\epsilon > 0\). This \(\epsilon\) is our convergence tolerance.
Experiments
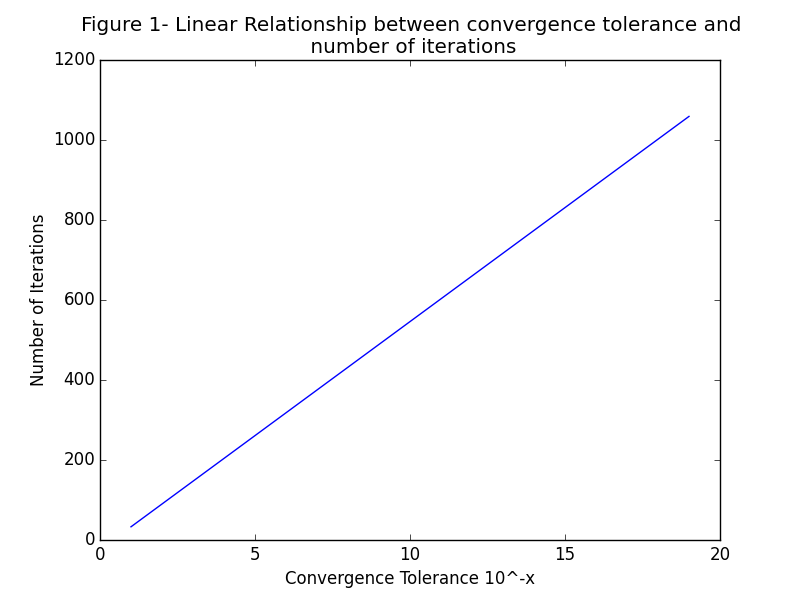
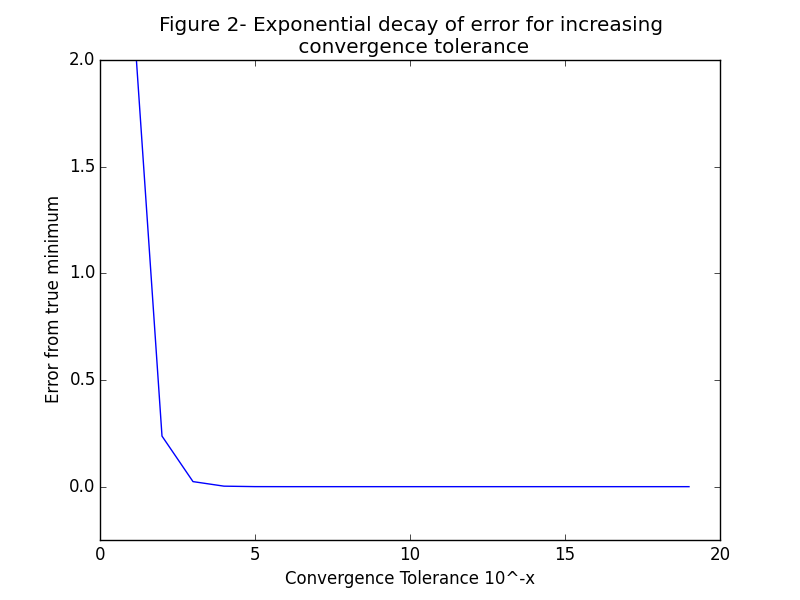
To demonstrate how convergence tolerance affects performance let’s take a simple example and set \(f(x) = x^2\). This example is nice because we know analytically that the minimum of this function is attained at \(x = 0\). Now we can study the effect of adjusting the convergence tolerance for a fixed learning rate. If we choose a learning rate of say \(\eta = .01\) and a starting point of \(x_0 = 3\) we can now plot how long it takes to converge vs how stringent our convergent tolerance is. In Figure 1 we see that for this particular problem there is a linear relationship between decreasing our convergence by \(10^{-x}\) and the number of iterations. This means that as we decrease our convergence tolerance the number of iterations scales linearly. Now iin Figure 2 we look at how much our error changes with an increasing convergence tolerance. We can see that the error decreases exponentially for this particular problem. This means that at a convergence tolerance of about \(10^{-4}\) we stop seeing significant gains in our estimated minimum. Putting these two ideas together we can say that after a certain point decreasing the convergence tolerance doesn’t provide much gain in performance but it still increases the amount of work we have to do by the same amount as before.