Introduction

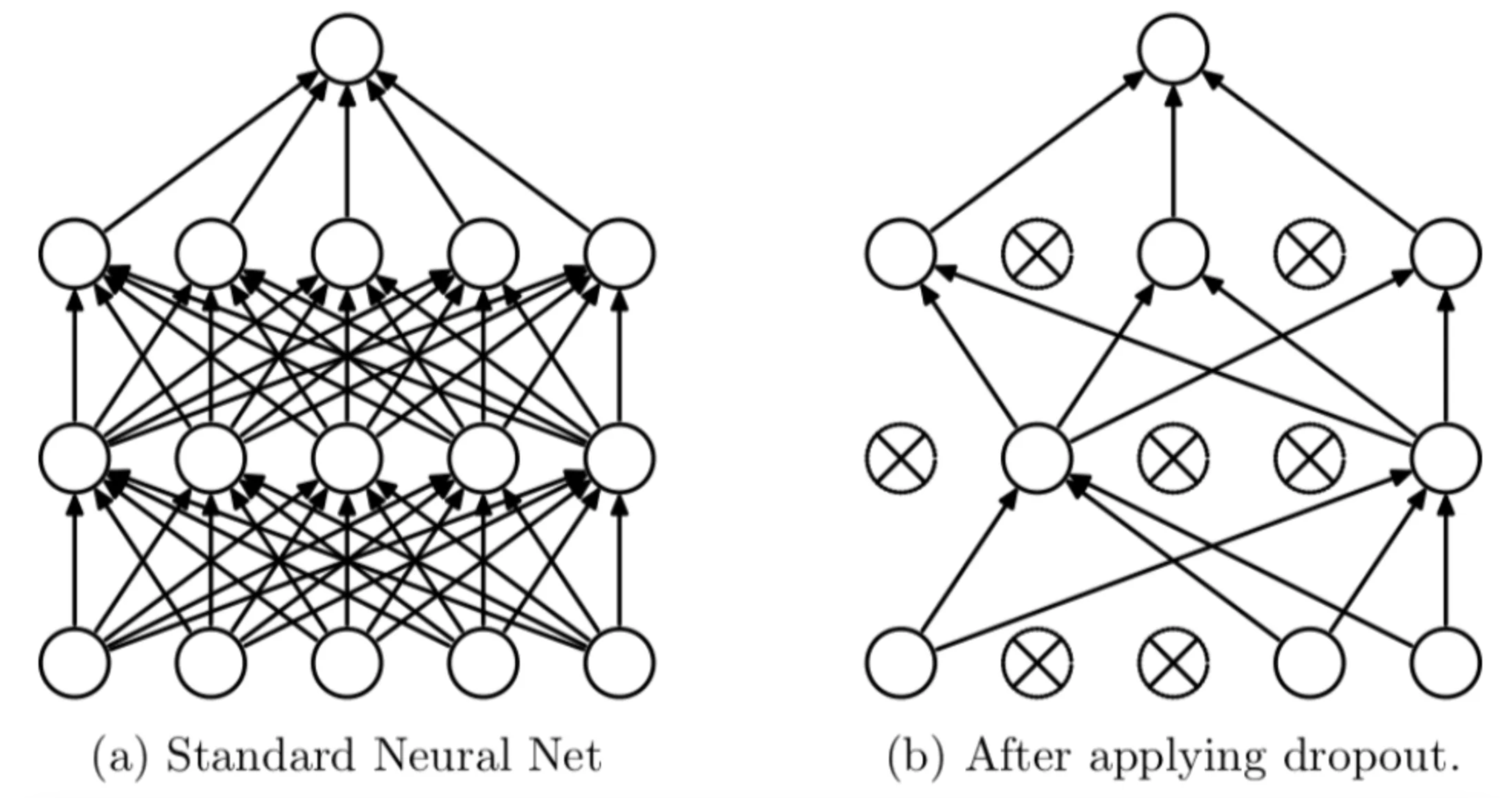
We’ve all heard of dropout. Historically it’s one of the most famous ways of regularizing a neural network, though nowadays it’s fallen somewhat out of favor and has been replaced by batch normalization. Regardless, it’s a cool technique and very simple to implement in PyTorch. In this quick blog post, we’ll implement dropout from scratch and show that we get similar performance to the standard dropout in PyTorch. A full notebook running all the experiments for this quick tutorial can be found here.

Appeal to Reader

If you pay for Medium, or haven’t used your free articles for this month, please consider reading this article there. I post all of my articles here for free so everyone can access them, but I also like beer and Medium is a good way to collect some beer money : ). So please consider buying me a beer by reading this article on Medium.

What is dropout?

Dropout is effectively randomly removing some nodes of a neural network during each training step. The idea is that this will help the network become more robust by not relying too heavily on any one node.

Effectively we ignore some random set of nodes on each training cycle. Pretty simple right?

Maths

So if we think about each layer in the network as a matrix we need only zero out a set of random nodes at each training step. This smells a lot like the Hadamard product. Think about a single-layer neural network where the layer is represented by a matrix A. This network will take a two-dimensional input and output a three-dimensional result so A is 2x3.

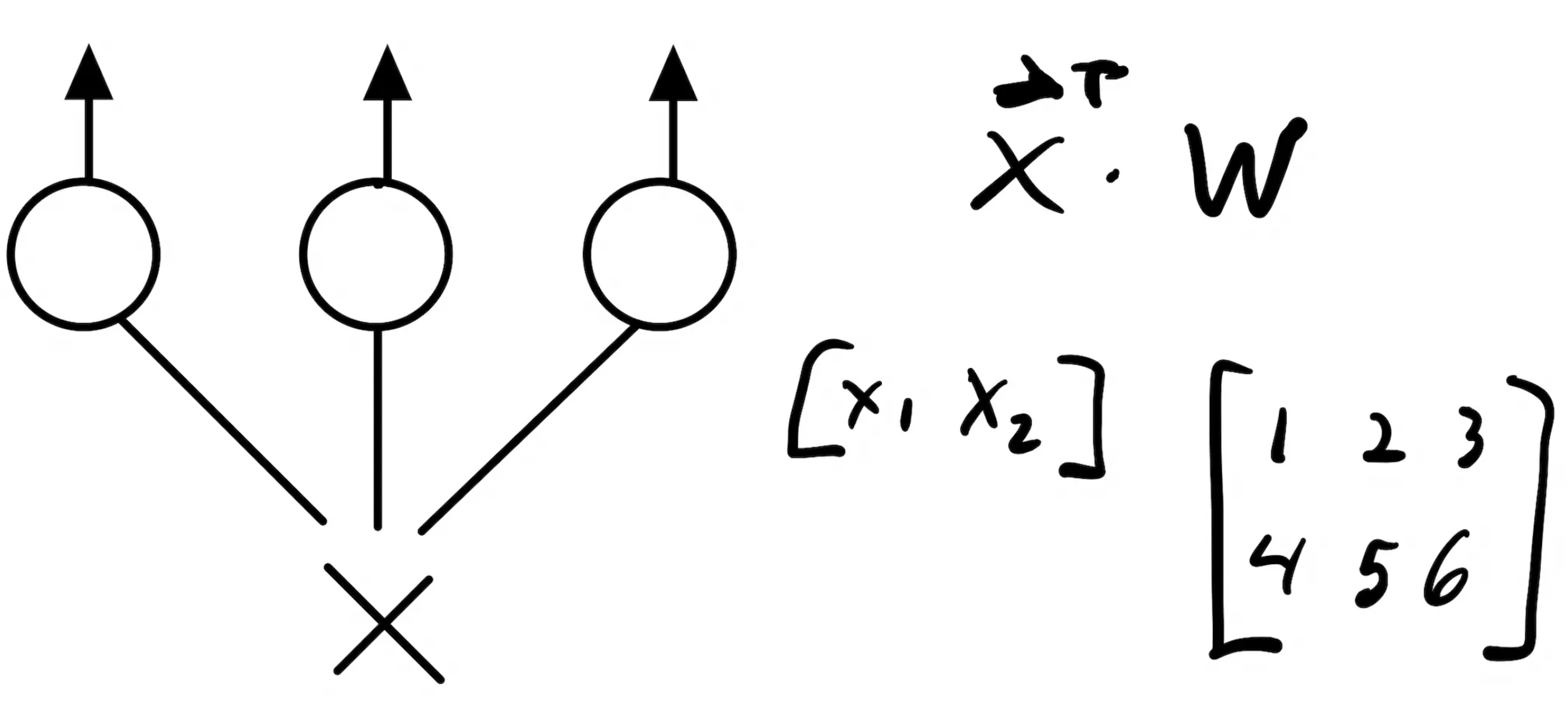
If we wanted to zero out some random set of nodes we can create a binary matrix D where each column is zero with probability p and then take the elementwise product. We can do this easily by creating a thresholded uniform vector with the same number of columns as A and then broadcasting in the multiplication.

Let’s implement this in PyTorch:

p = .5
A = torch.tensor([[1, 2, 3], [4, 5, 6]])
D = (torch.empty(A.size()[1]).uniform_(0, 1) >= p)
x = A.mul(D)
====Output===
tensor([[0, 2, 3],
        [0, 5, 6]])

As you can see, the above computation will drop out some random set of nodes.

An alternative is to do DropConnect where we drop out weights randomly instead of nodes. The only difference here is creating a random uniform matrix the same size as A instead of doing the broadcasting. This would look like this:

p = .5
A = torch.tensor([[1, 2, 3], [4, 5, 6]])
D = (torch.empty(A.size()).uniform_(0, 1) >= p)
x = A.mul(D)
====Output===
tensor([[1, 2, 0],
        [0, 5, 6]])

Implement a layer in PyTorch

With the initial math behind us, let’s implement a dropout layer in PyTorch.

class Dropout(torch.nn.Module):
    
    def __init__(self, p: float=0.5):
        super(Dropout, self).__init__()
        self.p = p
        if self.p < 0 or self.p > 1:
            raise ValueError("p must be a probability")
            
    def forward(self, x):
        if self.training:
            x = x.mul(torch.empty(x.size()[1]).uniform_(0, 1) >= self.p)
        return x

Lines 6–7 check to ensure that the probability passed to the layer is in fact a probability.

Line 10 determines if the layer is in training or testing mode. This matters because we don’t want to drop out nodes during inference only during training. This little if statement takes care of that for us.

Line 11 does all the magic we talked about earlier, it creates a binary matrix of the same size as x where there is a probability of p that any node is dropped out.

We can now use this dropout in a simple model.

class MNISTModel(torch.nn.Module):
    
    def __init__(self):
        super(MNISTModel, self).__init__()
        self.layer_1 = nn.Linear(28 * 28, 512)
        self.layer_2 = nn.Linear(512, 512)
        self.layer_3 = nn.Linear(512, 10)
        self.dropout = Dropout(.5)
    
    def forward(self, x):
        x = x.view(-1, 28 * 28)
        x = self.layer_1(x)
        x = self.layer_2(x)
        x = self.dropout(x)
        output = self.layer_3(x)
        return x

Training this model for two epochs yields a macro F1 score of 0.90 if we replace our custom dropout with the standard PyTorch dropout we get the same result. Pretty neat!

Final Note

The astute reader will notice that this isn’t quite the way dropout should work in practice. We aren’t normalizing by the number of times a node has been trained. Think about this for a second. When we drop out a bunch of random nodes some nodes will get trained more than others and should have different weights in the final predictions. We’d need to scale each node’s weights during inference time by the inverse of the keep probability 1/(1-p) to account for this. But that’s a pain to do at inference time. What most implementations do in practice is scale the weights during training by this amount. So the real dropout layer would look like this:

class TrueDropout(torch.nn.Module):
    
    def __init__(self, p: float=0.5):
        super(TrueDropout, self).__init__()
        self.p = p
        if self.p < 0 or self.p > 1:
            raise ValueError("p must be a probability")
            
    def forward(self, x):
        if self.training:
            x = x.mul(torch.empty(x.size()[1]).uniform_(0, 1) >= self.p) * (1 / (1 - self.p))
        return x

That’s it! Thanks for reading!